Cho tam giác cân ABC (AB = AC), đường phân giác góc B cắt AC tại D và cho biết AB = 15cm, BC = 10cm.
a. Tính AD, DC.
b. Đường vuông góc với BD tại B cắt đường thẳng AC kéo dài tại E. Tính EC.
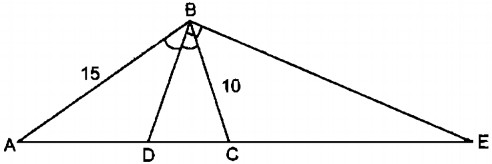

Vì BD là đường phân giác của \(\widehat {ABC}\) nên:
\({{AD} \over {DC}} = {{AB} \over {BC}}\) (tính chất đường phân giác )
Suy ra: \({{AD} \over {AD + DC}} = {{AB} \over {AB + BC}}\)
hay \({{AD} \over {AC}} = {{AB} \over {AB + BC}}\)
Advertisements (Quảng cáo)
Mà ∆ ABC cân tại A nên AC = AB = 15 (cm)
Suy ra: \({{AD} \over {15}} = {{15} \over {15 + 10}} \Rightarrow AD = {{15.15} \over {25}} = 9\) (cm)
Vậy DC = AC – AD = 15 – 9 = 6 (cm)
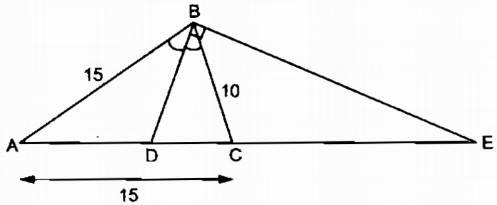
b. Vì BE ⊥ BD nên BE là đường phân giác góc ngoài tại đỉnh B
Suy ra: \({{EC} \over {EA}} = {{BC} \over {BA}}\) (tính chất đường phân giác )
Suy ra: \({{EC} \over {EC + AC}} = {{BC} \over {BA}} \Rightarrow EC.BA = BC\left( {EC + AC} \right)\)
Suy ra:
\(\eqalign{ & EC.BA - EC.BC = BC.AC \cr & \Rightarrow EC\left( {BA - BC} \right) = BC.AC \cr} \)
Vậy \(EC = {{BC.AC} \over {BA - BC}} = {{10.15} \over {15 - 10}} = 30\) (cm).
