Tam giác ABC có ba đường trung tuyến cắt nhau tại O. Gọi P, Q, R thứ tự là trung điểm của các đoạn thẳng OA, OB, OC.
Chứng minh rằng tam giác PQR đồng dạng với tam giác ABC.

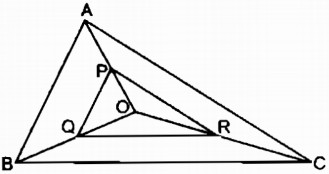
Trong ∆ OAB, ta có PQ là đường trung bình nên:
\(PQ = {1 \over 2}AB\) (tính chất đường trung bình của tam giác )
Suy ra: \({{PQ} \over {AB}} = {1 \over 2}\) (1)
Trong ∆ OAC, ta có PR là đường trung bình nên:
Advertisements (Quảng cáo)
\(PR = {1 \over 2}AC\) (tính chất đường trung bình của tam giác )
Suy ra: \({{PR} \over {AC}} = {1 \over 2}\) (2)
Trong ∆ OBC, ta có QR là đường trung bình nên:
\(QR = {1 \over 2}BC\) (tính chất đường trung bình của tam giác )
Suy ra: \({{QR} \over {BC}} = {1 \over 2}\) (3)
Từ (1), (2) và (3) suy ra: \({{PQ} \over {AB}} = {{PR} \over {AC}} = {{QR} \over {BC}}\)
Vậy ∆ PQR đồng dạng ∆ ABC (c.c.c).
