Cho trước tam giác ABC. Hãy dựng một tam giác đồng dạng với tam giác ABC theo tỉ số k. Câu 34 trang 91 Sách bài tập (SBT) Toán 8 tập 2 - Bài 5. Trường hợp đồng dạng thứ nhất (c.c.c)
Cho trước tam giác ABC. Hãy dựng một tam giác đồng dạng với tam giác ABC theo tỉ số k \( = {2 \over 3}\)
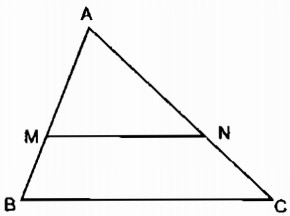
Cách dựng:
- Trên cạnh AB dựng điểm M sao cho AM = \({2 \over 3}\)AB
- Trên cạnh AC dựng điểm N sao cho AN = \({2 \over 3}\)AC
- Dựng đoạn thẳng MN ta được tam giác AMN đồng dạng với tam giác ABC theo tỉ số đồng dạng k = \({2 \over 3}\).
Advertisements (Quảng cáo)
Chứng minh:
Theo cách dựng ta có:
\(\eqalign{ & AM = {2 \over 3}AB \Rightarrow {{AM} \over {AB}} = {2 \over 3} \cr & AN = AC \Rightarrow {{AN} \over {AC}} = {2 \over 3} \cr} \)
Suy ra: \({{AM} \over {AB}} = {{AN} \over {AC}}\)
Theo định lí đảo của định lí Ta-lét ta có: MN // BC
Vậy ∆ AMN đồng dạng ∆ ABC và k \( = {{AM} \over {AB}} = {2 \over 3}\).