a. Hình thang cân ABCD có đáy nhỏ AB = b, đáy lớn CD = a, đường cao AH.
Chứng minh rằng (a và b có cùng đơn vị đo)
b. Tính đường cao của hình thang cân có hai đáy 10cm, 26cm và cạnh bên 17cm

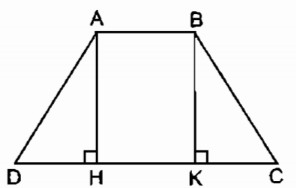
a. Kẻ đường cao BK
Xét hai tam giác vuông AHD và BKC, ta có:
\(\widehat {AHB} = \widehat {BKC} = {90^0}\)
AD = BC (tính chất hình thang cân)
\(\widehat D = \widehat C\) (gt)
Advertisements (Quảng cáo)
Do đó: ∆ AHD = ∆ BKC (cạnh huyền, góc nhọn)
⇒ HD = KC
Hình thang ABKH có hai cạnh bên song song nên AB = HK
a−b = DC – AB = DC – HK = HD + KC = 2HD
\( \Rightarrow HD = {{a - b} \over 2}\)
\(HD = DC-HD = a - {{a - b} \over 2} = {{a + b} \over 2}\)
b. \(HD = {{CD - AB} \over 2} = {{26 - 10} \over 2} = 8\left( {cm} \right)\)
Trong tam giác vuông AHD có \(\widehat {AHD} = {90^0}\)
\(A{D^2} = A{H^2} + H{D^2}\) (định lí Pi-ta-go)
\(\eqalign{
& \Rightarrow A{H^2} = A{D^2} - H{D^2} \cr
& A{H^2} = {17^2} - {8^2} = 289 - 64 = 225 \cr
& AH = 15(cm) \cr} \)
