Cho tam giác ABC có AB = 10cm, AC = 20cm. Trên cạnh AC, đặt đoạn thẳng AD = 5cm (h.25).. Câu 38 trang 92 Sách bài tập (SBT) Toán 8 tập 2 - Bài 6. Trường hợp đồng dạng thứ hai (c.g.c)
Cho tam giác ABC có AB = 10cm, AC = 20cm. Trên cạnh AC, đặt đoạn thẳng AD = 5cm.
Chứng minh \(\widehat {ABD} = \widehat {ACB}\).
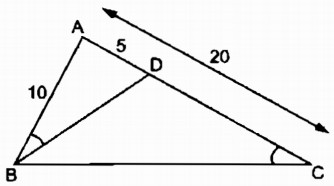

Ta có:
\(\eqalign{ & {{AD} \over {AB}} = {5 \over {10}} = {1 \over 2} \cr & {{AB} \over {AC}} = {{10} \over {20}} = {1 \over 2} \cr} \)
Advertisements (Quảng cáo)
Suy ra: \({{AD} \over {AB}} = {{AB} \over {AC}}\)
Xét ∆ ADB và ∆ ABC, ta có:
\(\widehat A\) chung
\({{AD} \over {AB}} = {{AB} \over {AC}}\) (chứng minh trên )
Suy ra: ∆ ADB đồng dạng ∆ ABC (c.g.c)
Vậy \(\widehat {ABD} = \widehat {ACB}.\)
