Cho đường thẳng d và hai điểm A, B có khoảng cách đến đường thẳng d theo thứ tự là 20cm và 6cm. Gọi C là trung điểm của AB. Tính khoảng cách từ C đến đường thẳng d.

a) Trường hợp A và B nằm trên một nửa mặt phẳng bờ chứa đường thẳng d.
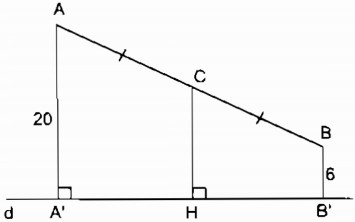
Gọi A’, B’ là chân đường vuông góc kẻ từ A và B đến d
AA’ ⊥ d; BB’ ⊥ d ⇒ AA’ // BB’
Tứ giác ABB’A’ là hình thang. Kẻ CH ⊥ d
⇒ CH // AA’ // BB’ nên CG là đường trung bình của hình thang ABB’A’
\( \Rightarrow CH = {{AA’ + BB’} \over 2} = {{20 + 6} \over 2} = 13\,\,\left( {cm} \right)\)
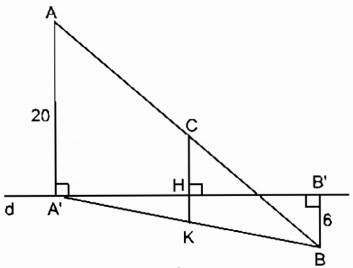
b) Trường hợp A và B nằm trên hai nửa mặt phẳng đối bờ chứa đường thẳng d
Advertisements (Quảng cáo)
Kẻ CH ⊥ d cắt A’B tại K
⇒ CH // AA’ // BB’
Trong ∆ AA’B ta có: AC = CB
Mà CK // AA’ nên A’K = KB và CK là đường trung bình của tam giác AA’B
\( \Rightarrow CK = {{AA’} \over 2}\) (tính chất đường trung bình của tam giác)
\(CK = {{20} \over 2} = 10\,\,\left( {cm} \right)\)
Trong ∆ A’BB’ có A’K = KB và KH // BB’
Nên KH là đường trung bình của ∆ A’BB’
\( \Rightarrow KH = {{BB’} \over 2}\) (tính chất đường trung bình của tam giác)
\( \Rightarrow KH = {6 \over 2} = 3\,\,\left( {cm} \right)\)
CH = CK – KH = 10 – 3 = 7(cm)
