Cho tam giác ABC, đường trung tuyến AM. Gọi D là trung điểm của AM, E là giao điểm của BD và AC. Câu 39 trang 84 Sách bài tập (SBT) Toán 8 tập 1 - Bài 4. Đường trung bình của tam giác của hình thang
Cho tam giác ABC, đường trung tuyến AM. Gọi D là trung điểm của AM, E là giao điểm của BD và AC. Chứng minh rằng \(AE = {1 \over 2}EC\).

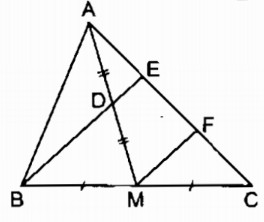
Gọi F là trung điểm của EC
Trong ∆ CBE ta có:
M là trung điểm của cạnh CB
F là trung điểm của cạnh CE
Nên MF là đường trung bình của ∆ CBE
Advertisements (Quảng cáo)
⇒ MF // BE (tính chất đường trung bình của tam giác)
Hay DE // MF
Trong tam giác AMF ta có:
D là trung điểm của AM
DE // MF
Suy ra: AE = EF (tính chất đường trung bình của tam giác)
Mà \(EF = FC = {{EC} \over 2}\0 nên \(AE = {1 \over 2}EC\).
