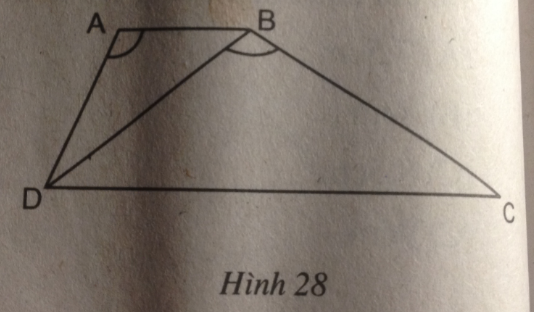
Hình thang ABCD (AB // CD) có AB = 2,5cm, AD = 3,5cm, BD = 5cm và \(\widehat {DAB} = \widehat {DBC}\) (h.28).
a. Chứng minh ∆ ADB đồng dạng ∆ BCD
b. Tính độ dài các cạnh BC, CD
c. Sau khi tính, hãy vẽ lại hình chính xác bằng thước và compa.
Giải:
(hình 28 trang 94 sbt)
Xét ∆ ABD và ∆ BDC, ta có:
Advertisements (Quảng cáo)
\(\widehat {DAB} = \widehat {DBC}\) (gt)
\(\widehat {ABD} = \widehat {BDC}\) (so le trong)
Suy ra: ∆ ABD đồng dạng ∆ BDC (g.g)
b. Vì ∆ ABD đồng dạng ∆ BDC nên : \({{AB} \over {BD}} = {{AD} \over {BC}} = {{BD} \over {DC}}\)
Với AB = 2,5; AD = 3,5; BD = 5, ta có:
\(\eqalign{ & {{2,5} \over 5} = {{3,5} \over {BC}} = {5 \over {DC}} \cr & \Rightarrow BC = {{5.3,5} \over {2,5}} = 7(cm) \cr} \)
Vậy DC = \({{5,5} \over {2,5}} = 10\) (cm)
