Cho tam giác vuông ABC (\(\widehat A = 90^\circ \)). Dựng AD vuông góc với BC (D thuộc BC). Đường phân giác BE cắt AD tại F (h.29).
Chứng minh: \({{FD} \over {FA}} = {{EA} \over {EC}}\).
Giải:
(hình 29 trang 94 sbt)
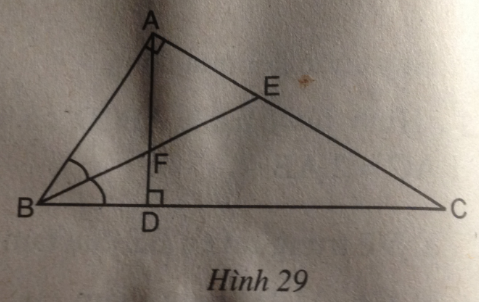
Trong tam giác ABC, ta có: BE là tia phân giác của góc ABC
Suy ra: \({{EA} \over {EC}} = {{AB} \over {BC}}\) (tính chất đường phân giác ) (1)
Trong tam giác ADB, ta có: BF là tia phân giác của góc ABD
Advertisements (Quảng cáo)
Suy ra: \({{FD} \over {FA}} = {{BD} \over {BA}}\) (tính chất đường phân giác ) (2)
Xét ∆ ABC và ∆ DAB, ta có:
\(\widehat {BAC} = \widehat {BDA} = 90^\circ \)
\(\widehat B\) chung
Suy ra: ∆ ABC đồng dạng ∆ DBA (g.g)
Suy ra: \({{BD} \over {BA}} = {{AB} \over {BC}}\) (3)
Từ (1), (2) và (3) suy ra: \({{FD} \over {FA}} = {{EA} \over {EC}}\)
