Chứng minh rằng, nếu hai tam giác ABC và A’B’C’ đồng dạng với nhau thì:
a. Tỉ số của hai đường phân giác tương ứng bằng tỉ số đồng dạng.
b. Tỉ số của hai trung tuyến tương ứng bằng tỉ số đồng dạng.

a. Vì ∆ ABC đồng dạng ∆ A’B’C’ nên ta có:
\(\widehat A = \widehat {A’};\widehat B = \widehat {B’}\) và \({{A’B’} \over {AB}} = k\)
Lại có: \(\widehat {BAD} = {1 \over 2}\widehat A\) (gt) và \(\widehat {B’A’D’} = {1 \over 2}\widehat A\) (gt)
Suy ra: \(\widehat {BAD} = \widehat {B’A’D’}\)
Xét ∆ ABD và ∆ A’B’D’, ta có:
\(\widehat B = \widehat {B’}\) (chứng minh trên )
\(\widehat {BAD} = \widehat {B’A’D’}\) (chứng minh trên )
Advertisements (Quảng cáo)
Suy ra: ∆ ABD đồng dạng ∆ A’B’D’ (g.g)
Vậy: \({{A’D’} \over {AD}} = {{A’B’} \over {AB}} = k\)
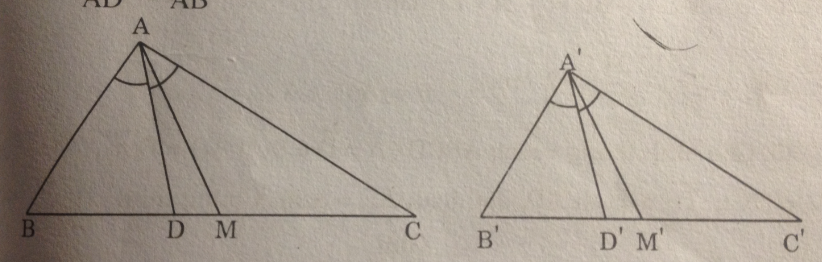
b. Vì ∆ ABC đồng dạng ∆ A’B’C’ nên \({{B’C’} \over {BC}} = k\)
Mà \(B’M’ = {1 \over 2}B’C’\) và \(BM = {1 \over 2}BC\) nên \({{B’M’} \over {BM}} = k\)
Xét ∆ ABM và ∆ A’B’M’, ta có:
\({{A’B’} \over {AB}} = {{B’M’} \over {BM}} = k\)
\(\widehat B = \widehat {B’}\) (chứng minh trên )
Suy ra: ∆ ABM đồng dạng ∆ A’B’M’ (c.g.c)
Vậy \({{AM’} \over {AM}} = {{A’B’} \over {AB}} = k\)
