Tam giác vuông ABC có $\widehat A = 90^\circ $ và đường cao AH. Từ điểm H hạ đường HK vuông góc với AC (h.27).
a. Hỏi trong hình đã cho có bao nhiêu tam giác đồng dạng với nhau ?
b. Hãy viết các cặp tam giác đồng dạng với nhau theo thứ tự các đỉnh tương ứng và viết tỉ lệ thức giữa các cặp cạnh tương ứng của chúng.
Giải:
(hình 27 trang 93 sbt)
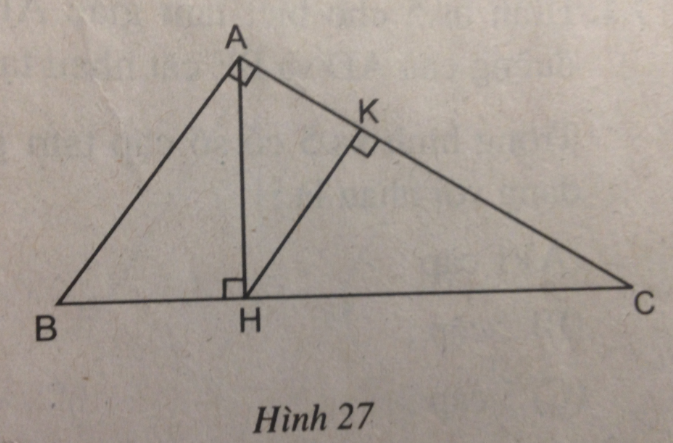
a. Trong hình bên có 5 tam giác đồng dạng với nhau theo từng đôi một, đó là: ∆ABC; ∆ HAB; ∆ HAC; ∆ KAH; ∆ KHC.
b. Các cặp tam giác đồng dạng với nhau theo thứ tự các đỉnh tương ứng và viết tỉ lệ thức giữa các cặp cạnh tương ứng của chúng:
- ∆ ABC đồng dạng ∆ HAB. Ta có: \({{AB} \over {HA}} = {{AC} \over {HB}} = {{BC} \over {AB}}\)
Advertisements (Quảng cáo)
- ∆ ABC đồng dạng ∆ HAC . Ta có: \({{AB} \over {HA}} = {{AC} \over {HC}} = {{BC} \over {AC}}\)
- ∆ ABC đồng dạng ∆ KHC. Ta có: \({{AB} \over {KH}} = {{AC} \over {KC}} = {{BC} \over {HC}}\)
- ∆ ABC đồng dạng ∆ KAH. Ta có: \({{AB} \over {KA}} = {{AC} \over {KH}} = {{BC} \over {AH}}\)
- ∆ HAB đồng dạng ∆ HAC. Ta có: \({{HB} \over {HA}} = {{HA} \over {HC}} = {{BA} \over {AC}}\)
- ∆ HAB đồng dạng ∆ KHC. Ta có: \({{HB} \over {KH}} = {{HA} \over {KC}} = {{BA} \over {HC}}\)
- ∆ HAB đồng dạng ∆ KAH. Ta có: \({{HB} \over {KA}} = {{HA} \over {KH}} = {{BA} \over {AH}}\)
- ∆ HAC đồng dạng ∆ KHC. Ta có: \({{HA} \over {KH}} = {{HC} \over {KC}} = {{AC} \over {HC}}\)
- ∆ HAC đồng dạng ∆ KAH. Ta có: \({{HA} \over {KA}} = {{HC} \over {KH}} = {{AC} \over {AH}}\)
- ∆ KHC đồng dạng ∆ KAH. Ta có: \({{KH} \over {KA}} = {{KC} \over {KH}} = {{HC} \over {AH}}\)
