Hình thang ABCD có AB // CD, AB = a, BC = b, CD = c, DA = d. Các đường phân giác của các góc ngoài đỉnh A và D cắt nhau tại M, các đường phân giác của các góc ngoài đỉnh B và C cắt nhau tại N.
a) Chứng ninh rằng MN // CD.
b) Tính độ dài MN theo a, b, c, d (a, b, c, d có cùng đơn vị đo)

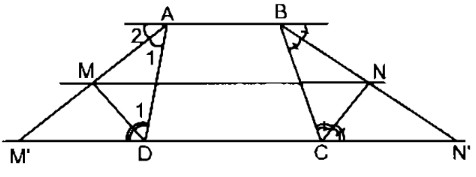
a) Gọi M’ và N’ là giao điểm của tia AM và BN với CD. Ta có:
\(\widehat {M’} = {\widehat A_2}\) (so le trong)
\({\widehat A_1} = {\widehat A_2}\) (gt)
Suy ra: \(\widehat {M’} = {\widehat A_1}\)
Nên ∆ ADM’ cân tại D
DM là phân giác của \(\widehat {ADM’}\)
Suy ra: DM là đường trung tuyến (tính chất tam giác cân)
⇒ AM = MM’
Advertisements (Quảng cáo)
\(\widehat {N’} = {\widehat B_2}\) (so le trong)
\({\widehat B_1} = {\widehat B_2}\) (gt)
Suy ra: \(\widehat {N’} = {\widehat B_1}\) nên ∆ BCN’ cân tại C
CN là phân giác của \(\widehat {BCN’}\)
Suy ra: CN là đường trung tuyến (tính chất tam giác cân)
⇒ BN = NN’
Suy ra: MN là đường trung bình của hình thang ABN’M’
⇒ MN // M’N’ (tính chất đường trung bình hình thang)
Hay MN // CD
b) \(MN = {{AB + M’N’} \over 2}\) (tính chất đường trung bình của hình thang)
\( \Rightarrow MN = {{AB + M’D + CD + CN’} \over 2}\,\,\,\,\,\,\,\,\,\,\left( 1 \right)\)
Mà M’D = AD, CN’ = BC. Thay vào (1):
\(MN = {{AB + AD + CD + BC} \over 2} = {{a + d + c + b} \over 2}\)
