Gọi M là trung điểm của BC, I là giao điểm của BD và AM. Chứng minh rằng AI = IM.. Câu 34 trang 84 Sách bài tập (SBT) Toán 8 tập 1 - Bài 4. Đường trung bình của tam giác của hình thang
Cho tam giác ABC, điểm D thuộc cạnh AC sao cho \(AD = {1 \over 2}DC\). Gọi M là trung điểm của BC, I là giao điểm của BD và AM. Chứng minh rằng AI = IM.

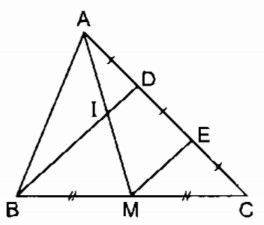
Gọi E là trung điểm của DC
Trong ∆ BDC ta có:
M là trung điểm của BC (gt)
E là trung điểm của CD (gt)
Nên ME là đường trung bình của ∆ BCD
Advertisements (Quảng cáo)
⇒ ME // BD( tính chất đường trung bình của tam giác)
Suy ra: DI // ME
\(AD = {1 \over 2}DC\) (gt)
\(DE = {1 \over 2}DC\) (theo cách vẽ)
⇒AD = DE
DI // ME
Nên AI = IM (tính chất đường trung bình của tam giác)
