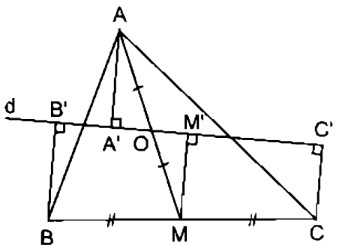
Cho tam giác ABC, đường trung tuyến AM. Gọi O là trung điểm của AM. Qua O kẻ đường thẳng d cắt các cạnh AB và AC. Gọi AA’, BB’, CC’ là các đường vuông góc kẻ từ A, B, C đến đường thẳng d. Chứng minh rằng:
\({\rm{AA’ = }}{{BB’ + CC’} \over 2}\)

Ta có: BB’ ⊥ d (gt)
CC’ ⊥ d (gt)
Suy ra: BB’ // CC’
Tứ giác BB’CC’ là hình thang
Kẻ MM’ ⊥ d
⇒ MM’ // BB’ // CC’
Advertisements (Quảng cáo)
Nên MM’ là đường trung bình của hình thang BB’CC’
\( \Rightarrow MM’ = {{BB’ + CC’} \over 2}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 1 \right)\)
Xét hai tam giác vuông AA’O và MM’O:
\(\widehat {OA’A} = \widehat {OM’M}\)
AO = MO (gt)
\(\widehat {AOA’} = \widehat {MOM’}\) (đối đỉnh)
Do đó: ∆ AA’O = ∆ MM’O (cạnh huyền, góc nhọn)
⇒ AA’ = MM’ (2)
Từ (1) và (2) suy ra: \({\rm{AA’ = }}{{BB’ + CC’} \over 2}\).
