Tính diện tích tam giác AMH, biết rằng BH = 4cm, CH = 9cm.. Câu 50 trang 96 Sách bài tập (SBT) Toán 8 tập 2 - Bài 8. Các trường hợp đồng dạng của tam giác vuông
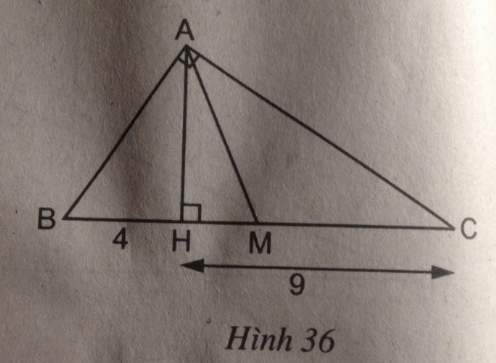
Tam giác vuông ABC (\(\widehat A = 90^\circ \)) có đường cao AH và trung tuyến AM (h.36). Tính diện tích tam giác AMH, biết rằng BH = 4cm, CH = 9cm.
Giải:
(hình 36 trang 96 sbt)
Xét hai tam giác vuông HBA và HAC, ta có:
\(\widehat {BHA} = \widehat {AHC} = 90^\circ \)
\(\widehat C = \widehat {HAC}\) (hai góc cùng phụ góc C)
Advertisements (Quảng cáo)
Suy ra: ∆ HBA đồng dạng ∆ HAC (g.g)
Suy ra: ${{HA} \over {HB}} = {{HC} \over {HA}}\)
\( \Rightarrow H{A^2} = HB.HC = 4.9 = 36\) (cm)
Suy ra: AH = 6(cm)
Lại có: \(BM = {1 \over 2}BC = {1 \over 2}.\left( {9 + 4} \right) = {1 \over 2}.13 = 6,5\) (cm)
Mà \(HM = BM - BH = 6,5 - 4 = 2,5\) (cm)
Vậy \({S_{AHM}} = {1 \over 2}AH.HM = {1 \over 2}.6.2,5 = 7,5(c{m^2})\)