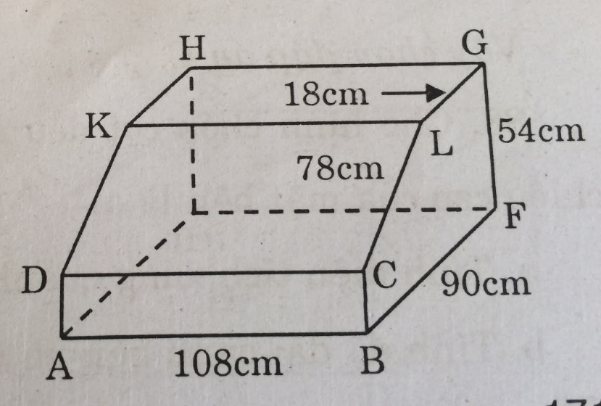
Người ta vẽ phần trên của một cái bàn học có dạng một lăng trụ đứng theo hình 165. Các kích thước của nó là:
AB = 108cm, BC = 24cm, BF = 90cm, FG = 54cm, LG = 18cm, LC = 78cm.
Các cạnh AB, DC, EF, HG và KL đều vuông góc với mặt phẳng (ADKHE) và LG song song với BF.
Hãy tính:
a. Diện tích hình chữ nhật CDKL;
b. Diện tích hình thang BCLGF;
c. Thể tích hình lăng trụ đứng ADKHE.BCLGF.
Giải:
(hình 165 trang 157 sbt)
a. Diện tích hình chữ nhật CDKL:
CD = AB = 108 (cm)
\(\eqalign{ & {S_{CDKL}} = CD.CL \cr & = 108.78 = 8424(c{m^2}) \cr} \)
Advertisements (Quảng cáo)
b. Hình BCLGF có thể chia thành hai hình. Một hình chữ nhật có kích thước 18cm và 54cm, một hình thang vuông có 2 đáy là 24cm và 54cm, chiều cao 72cm.
Diện tích phần hình chữ nhật là:
\(S = 18.54 = 972(c{m^2})\)
Diện tích phần hình thang vuông:
\(S = \left[ {\left( {24 + 54} \right):2} \right].72 = 2808(c{m^2})\)
Diện tích hình BCLGF bằng: 972 + 2808 = 3780 (cm2)
c. Hình lăng trụ đứng ADKHE.BCLGF có thể chia thành hai hình. Một hình hộp chữ nhật có hai cạnh đáy là 18cm và 54cm, chiều cao hình hộp 108cm, một hình lăng trụ đứng đáy hình thang vuông với hai cạnh đáy 24cm và 54cm, chiều cao đáy 72cm, chiều cao lăng trụ 108cm.
Thể tích phần hình hộp chữ nhật là:
\(V = 18.54.108 = 104976(c{m^3})\)
Thể tích phần hình lăng trụ đứng là:
\(V = S.h = 2808.108 = 303264(c{m^3})\)
Thể tích lăng trụ đứng ADKHE.BCLGF bằng:
\(V = 104976 + 303264 = 408240(c{m^3})\)
