Cho hình chóp cụt tứ giác đều ABCD.A’B’C’D’ có các cạnh đáy là a và 2a, chiều cao của mặt bên là a.
a. Tính diện tích xung quanh của hình chóp cụt.
b. Tính độ dài cạnh bên và chiều cao hình chóp cụt.

(hình trang 173 sgbt)
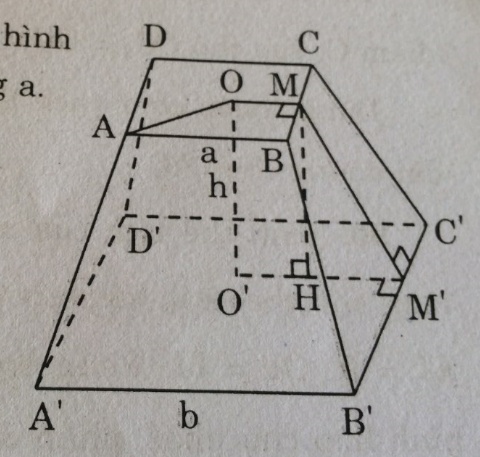
a. Một mặt bên của hình chóp cụt là một hình thang có hai đáy là a và 2a; đường cao bằng a.
Diện tích mặt bên là:
\(S = \left( {a + 2a} \right):2.a = {3 \over 2}{a^2}\) (đvdt)
Diện tích xung quanh hình nón cụt:
\({S_{xq}} = 4.{3 \over 2}{a^2} = 6{a^2}\) (đvdt)
Advertisements (Quảng cáo)
b. Kẻ A’H ⊥ AB
Ta có K là trung điểm của AB, I là trung điểm của A’B’, O và O’ là tâm của hai hình vuông đáy.
Ta có: \(A’I = {a \over 2};AK = a \Rightarrow AH = {a \over 2}\)
Áp dụng định lí Pi-ta-go vào tam giác vuông AA’H, ta có:
\(A'{A^2} = A'{H^2} + A{H^2} = {a^2} + {{{a^2}} \over 4} = {{5{a^2}} \over 4}\)
Suy ra: \(AA’ = \sqrt {{{5{a^2}} \over 4}} \)
Kẻ IE ⊥ OK, ta có: OK = a \( \Rightarrow EK = {a \over 2}\)
Áp dụng định lí Pi-ta-go vào tam giác vuông IEK, ta có:
\(I{K^2} = I{E^2} + E{K^2} = {a^2} - {\left( {{a \over 2}} \right)^2} = {{3{a^2}} \over 4}\)
Vậy \(IE = \sqrt {{{3{a^2}} \over 4}} \)
