
Bạn Nam dùng 6 đoạn tre vót thẳng để làm khung diều hình thoi. Trong đó có 2 đoạn tre dài 60cm và 80cm để làm hai đường chéo của cái diều, 4 đoạn tre còn lại là 4 cạnh của cái diều, Khi đó tổng độ dài 4 đoạn tre dùng làm cạnh của cái diều hình thoi là:
A. 5m
B. 1m
C. 1,5m
D. 2m

Áp dụng tính chất của hình thoi và ĐL Pythagore để tính độ dài cạnh hình thoi

Advertisements (Quảng cáo)
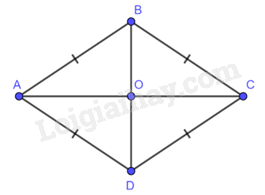
Giả sử hình thoi \(ABCD\) có hai đường chéo \(AC = 80\)cm; \(BD = 60\)cm
Suy ra:
\(BD \bot AC\) hay \(\widehat {BOA} = 90^\circ \)
\(OA = OC = \frac{1}{2}AC = \frac{1}{2}.80 = 40\)cm;
\(OB = OD = \frac{1}{2}BD = \frac{1}{2}.60 = 30\)cm
Áp dụng định lý Pythagore vào tam giác vuông \(BOA\) nên ta có:
\(A{B^2} = O{B^2} + O{A^2} = {30^2} + {40^2} = 900 + 1600 = 2500 = {50^2}\)
\(AB = 50\) (cm)
Chu vi hình thoi là: \(50.4 = 200\) (cm) \( = 2\) (m)
Tổng độ dài bốn đoạn tre dùng làm cạnh của cái diều là 2m
