
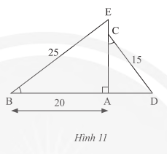
Trong Hình 11, cho biết \(\widehat B = \widehat C,BE = 25cm,AB = 20cm,DC = 15cm\). Tính độ dài đoạn thẳng \(CE\).

- Nếu một tam giác vuông này có một góc nhọn bằng góc nhọn của tam giác vuông kia thì hai tam giác vuông đó đồng dạng với nhau.
- Hai tam giác đồng dạng sẽ có các cặp cạnh tương ứng có cùng tỉ lệ.
- Định lí Py – ta – go.

Xét \(\Delta ABE\) và \(\Delta ACD\) có:
\(\widehat {EBA} = \widehat {ACD}\) (giả thuyết)
Advertisements (Quảng cáo)
\(\widehat {BAE} = \widehat {CAD} = 90^\circ \)
Do đó, \(\Delta ABE\backsim\Delta ACD\) (g.g)
Vì \(\Delta ABE\backsim\Delta ACD\) nên \(\frac{{AB}}{{AC}} = \frac{{EB}}{{CD}}\) (các cặp cạnh tương ứng)
Thay số, \(\frac{{20}}{{AC}} = \frac{{25}}{{15}} \Rightarrow AC = \frac{{20.15}}{{25}} = 12\)cm.
Áp dụng định lí Py – ta – go cho \(\Delta ABE\) vuông tại \(A\) ta có:
\(B{E^2} = A{E^2} + A{B^2} \\\Leftrightarrow A{E^2} = B{E^2} - A{B^2} = {25^2} - {20^2} = 225 \\\Rightarrow AE = \sqrt {225} = 15cm\)
Độ dài \(CE\) là:
15 – 12 = 3cm
Vậy \(CE = 3cm.\)
