Bài 5 trang 76 Toán 8 tập 2– Chân trời sáng tạo: Quan sát Hình 1Chứng minh rằng: \(\Delta ABH\backsim\Delta DCB\); \(\frac{{BC}}{{BE}} = \frac{{BD}}{{BA}}\)...

Quan sát Hình 12. Chứng minh rằng:

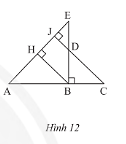
a) \(\Delta ABH\backsim\Delta DCB\);

b) \(\frac{{BC}}{{BE}} = \frac{{BD}}{{BA}}\).

- Nếu một tam giác vuông này có một góc nhọn bằng góc nhọn của tam giác vuông kia thì hai tam giác vuông đó đồng dạng với nhau.

a) Vì \(\left\{ \begin{array}{l}JC \bot AE\\BH \bot AE\end{array} \right. \Rightarrow JC//BH\). Vì \(JC//BH \Rightarrow \widehat {HBA} = \widehat {JCA}\) (hai góc đồng vị)

hay \(\widehat {HBA} = \widehat {DCB}\)

Xét \(\Delta ABH\) và \(\Delta DCB\) có:

\(\widehat {HBA} = \widehat {DCB}\) (chứng minh trên)

\(\widehat {AHB} = \widehat {DBC} = 90^\circ \)

Do đó, \(\Delta ABH\backsim\Delta DCB\) (g.g)

b) Vì (hai góc tương ứng) hay \(\widehat {EAB} = \widehat {CDB}\).

Xét \(\Delta AEB\) và \(\Delta DCB\) có:

\(\widehat {EAB} = \widehat {CDB}\) (chứng minh trên)

\(\widehat {ABE} = \widehat {DBC} = 90^\circ \)

Do đó, \(\Delta AEB\backsim\Delta DCB\) (g.g)

Suy ra, \(\frac{{BE}}{{BC}} = \frac{{BA}}{{BD}}\) (các cặp cạnh tương ứng có cùng tỉ lệ)

Hay \(\frac{{BC}}{{BE}} = \frac{{BD}}{{BA}}\) (điều phải chứng minh).