Cho hình bình hành \(ABCD\). Gọi \(I\) và \(K\) lần lượt là trung điểm của các cạnh \(AB\) và \(CD\); \(E\) và \(F\) lần lượt là giao điểm của \(AK\) và \(CI\) với \(BD\).
a) Chứng minh tứ giác \(AEFI\) là hình thang
b) Chứng minh \(DE = EF = FB\)
a) Áp dụng dấu hiệu nhận biết hình thang
b) Áp dụng tính chất của trọng tâm
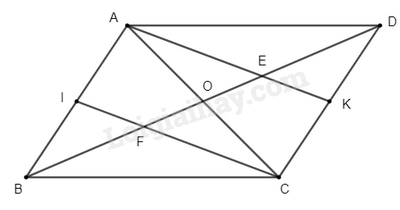
a) Vì \(ABCD\) là hình bình hành (gt)Suy ra \(AB\) // \(CD\), \(AD\) // \(BC\); \(AB = CD\); \(AD = BC\)Mà \(IA = IB = \frac{{AB}}{2}\); \(KD = KC = \frac{{CD}}{2}\) (do \(I\),\(K\) là trung điểm)Suy ra \(IA = IB = KD = KC\)Xét tứ giác \(AKCI\) có:\(AI = KC\) (cmt)\(AI\) // \(KC\)Suy ra \(AKCI\) là hình bình hànhSuy ra \(IC\) // \(AK\)Hay \(IF\) // \(AE\)Suy ra \(AEFI\) là hình thangb) Vì \(ABCD\), \(AKCI\) là hình bình hành (gt)Suy ra \(O\) là trung điểm của \(AC\), \(BD\), \(KI\)Suy ra \(OD = OB = \frac{1}{2}BD\) (1)Xét tam giác \(ADC\) có hai trung tuyến \(AK\), \(DO\) cắt nhau tại \(E\)Suy ra \(E\) là trọng tâm của tam giácSuy ra \(ED = \frac{2}{3}DO\) (2)Chứng minh tương tự ta có \(BF = \frac{2}{3}BO\) (3)Từ (1), (2), (3) suy ra \(ED = BF = \frac{1}{3}BD\)Suy ra \({\rm{EF}} = \frac{1}{3}BD\)Vậy \(DE = EF = FB\)