
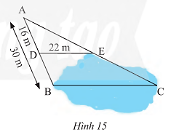
Người ta ứng dụng hai tam giác đồng dạng để đo khoảng cách \(BC\) ở hai điểm không thể đến được (hình 15). Biết \(DE//BC\).
a) Chứng minh rằng \(\Delta ADE\backsim\Delta ABC\).
b) Tính khoảng cách \(BC\).

- Nếu một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh còn lại thì nó tạo thành một tam giác mới đồng dạng với tam giác đã cho.
- Nếu \(\Delta A’B’C’\backsim\Delta ABC\)theo tỉ số \(k\)thì \(\left\{ \begin{array}{l}\widehat A = \widehat {A’};\widehat B = \widehat {B’};\widehat C = \widehat {C’}\\\frac{{A’B’}}{{AB}} = \frac{{A’C’}}{{AC}} = \frac{{B’C’}}{{BC}} = k\end{array} \right.\)
Advertisements (Quảng cáo)

a) Xét tam giác \(ABC\) ta có:
\(DE//BC\) và \(D,E\) cắt \(AB;AC\) tại \(D;E\).
Do đó, \(\Delta ADE\backsim\Delta ABC\) (định lí)
b) Vì \(\Delta ADE\backsim\Delta ABC\) nên \(\frac{{AD}}{{AB}} = \frac{{DE}}{{BC}}\) (cách cặp cạnh tương ứng có cùng tỉ lệ).
Thay số, \(\frac{{16}}{{30}} = \frac{{22}}{{BC}} \Rightarrow BC = \frac{{22.30}}{{16}} = 41,25\)
Vậy \(BC = 41,25m\).
