Hoạt động 1
Cho một tam giác vuông có hai cạnh góc vuông là \(a\), \(b\) và cạnh huyền là \(c\).
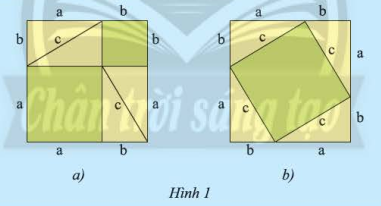
- Lấy một tờ bìa lớn, cắt tám hình tam giác vuông bằng tam giác vuông đã cho và cắt hai hình vuông lớn có cùng có cạnh bằng \(a + b\).
- Đặt bốn tam giác vuông lên hình vuông thứ nhất trong Hình 1a. Phần bìa không bị che lấp gồm hai hình vuông có cạnh lần lượt là \(a\) và \(b\). Tính diện tích phần bìa đó là \(a\) và \(b\).
- Đặt bốn tam giác vuông còn lại lên hình vuông thứ hai như trong Hình 1b. Phần bìa không bị che lấp là hình vuông có cạnh là \(c\). Tính diện tích phần bìa đó theo \(c\).
- Rút ra kết luận về quan hệ giữa \({a^2} + {b^2}\) và \({c^2}\).

Sử dụng công thức rồi tính diện tích theo yêu cầu

- Diện tích hai hình vuông màu xanh trong hình 1a là: \({a^2} + {b^2}\)
- Diện tích hình vuông màu xanh trong hình 1b là: \({c^2}\)
- Vậy \({a^2} + {b^2} = {c^2}\)
Thực hành 1
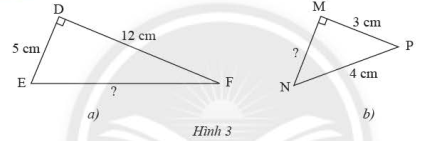
Tính độ dài cạnh \(EF\), \(MN\) của các tam giác vuông trong hình 3.

Sử dụng định lý Pythagore để tính độ dài các cạnh còn lại của tam giác vuông.

a) Áp dụng định lý Pythagore vào tam giác vuông \(DEF\) ta có:
\(E{F^2} = D{E^2} + D{F^2}\)
Advertisements (Quảng cáo)
\(E{F^2} = {5^2} + {12^2} = 25 + 144 = 169 = {13^2}\)
Vậy \(EF = 13\) (cm)
b) Áp dụng định lý Pythagore vào tam giác vuông \(MNP\) ta có:
\(M{N^2} + M{P^2} = N{P^2}\)
\(M{N^2} + {3^2} = {4^2}\)
\(M{N^2} + 9 = 16\)
\(M{N^2} = 16 - 9 = 7\)
\(MN = \sqrt 7 \) (cm)
Vận dụng 1
Một chiếc ti vi màn hình phẳng có chiều rộng và chiều dài đo được lần lượt là \(72\)cm và \(120\)cm. Tính độ dài đường chéo của màn hình chiếc ti vi đó theo đơn vị inch (biết 1 inch \( \approx \)\(2,54\)cm).


Sử dụng định lý Pythagore tính độ dài đường chéo của màn hình chiếc tivi.

Gọi \(a\), \(b\), \(c\) là độ dài chiều dài, chiều rộng và đường chéo của tivi (đơn vị: cm)
Áp dụng định lí Pythagore ta có:
\({c^2} = {a^2} + {b^2}\)
\({c^2} = {120^2} + {72^2} = 14400 + 5184 = 19584\)
\(c = 24\sqrt {34} \) (cm)
Độ dài đường chéo của màn hình chiếc ti vi đó theo đơn vị inch là:
\(24\sqrt {34} :2,54 \approx 54\) (inch)
