Luyện tập - Chủ đề 4 : Hình chóp đều - Bài tập 10 trang 123 Tài liệu dạy – học Toán 8 tập 2. Giải bài tập Cho hình chóp tứ giác đều có cạnh đáy bằng a và cạnh bên dài 2a. Tính theo a độ dài đường cao của hình chóp.
Cho hình chóp tứ giác đều có cạnh đáy bằng a và cạnh bên dài 2a. Tính theo a độ dài đường cao của hình chóp.
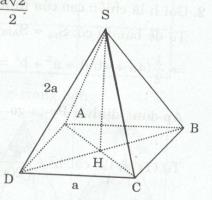
ABCD là tứ giác đều => ABCD là hình vuông \( \Rightarrow AD \bot AB\) tại A
\( \Rightarrow D{B^2} = A{D^2} + A{B^2}\) (định lí Py-ta-go)
Advertisements (Quảng cáo)
\( \Rightarrow D{B^2} = 2{a^2} \Rightarrow DB = a\sqrt 2 ,\) mà \(DH = {{DB} \over 2} \Rightarrow DH = {{a\sqrt 2 } \over 2}\)
∆SDH vuông tại H có: \(S{H^2} + D{H^2} = S{D^2}\) (định lí Py-ta-go)
\(\eqalign{ & \Rightarrow S{H^2} + {{{a^2}} \over 2} = {(2a)^2} \cr&\Rightarrow S{H^2} = 4{a^2} - {{{a^2}} \over 2} = {{7{a^2}} \over 2} \cr & \Rightarrow SH = {{\sqrt {14} } \over 2}a \cr} \)
Vậy độ dài đường cao của hình chóp là \({{\sqrt {14} } \over 2}a\)