
Tính diện tích toàn phần của:
a) Hình chóp tam giác đều có tất cả các cạnh đều bằng 10 cm.
b) Hình chóp lục giác đều, biết cạnh đáy a = 12 cm, cạnh bên b = 20 cm.

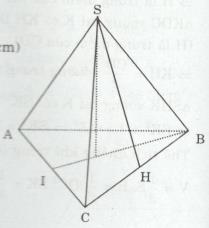
a) Chiều cao của tam giác đáy là:
\(IB = \sqrt {B{C^2} - I{C^2}} = \sqrt {{{10}^2} - {{\left( {{{10} \over 2}} \right)}^2}} \)\(\,= \sqrt {{{10}^2} - {5^2}} = \sqrt {75} (cm)\)
Diện tích đáy của hình chóp là:
\({S_d} = {1 \over 2}BI.AC = {1 \over 2}\sqrt {75} .10 \)\(\,= 5\sqrt {75} (c{m^2})\)
Kẻ \(SH \bot BC\) tại H
∆SBC cân tại S => SH là đường trung tuyến
=> H là trung điểm của BC \( \Rightarrow BH = {{BC} \over 2} = 5(cm)\)
∆SBH vuông tại H có \(S{H^2} + H{B^2} = S{B^2}\) (định lí Py-ta-go)
\( \Rightarrow S{H^2} + {5^2} = {10^2} \Rightarrow S{H^2} = 75 \)
\(\Rightarrow SH = 5\sqrt 3 (cm)\)
Advertisements (Quảng cáo)
Diện tích xung quanh của hình chóp:
\({S_{xq}} = p.d = {1 \over 2}.3BC.SH \)\(\,= {1 \over 2}.3.10.\sqrt {75} = 15\sqrt {75} (c{m^2})\)
Diện tích toàn phần của hình chóp:
\({S_{tp}} = {S_{xq}} + {S_d} = 15\sqrt {75} + 5\sqrt {75} \)\(\, = 20\sqrt {75} (c{m^2})\)
b) Vì MNOPQR là lục giác đều, nên các tam giác MHN, NHO, OHP, PHQ, QHR và RHM là sáu tam giác đều bằng nhau
Đường cao \(HK = \sqrt {H{R^2} - K{R^2}} \)\(\, = \sqrt {{{12}^2} - {6^2}} = \sqrt {108} (cm)\)
Diện tích đáy của hình chóp:
\({S_d} = 6{S_{MHR}} = 6.{1 \over 2}KH.MR\)\(\, = 3.\sqrt {108} .12 = 36\sqrt {108} (c{m^2})\)
Đường cao của mỗi mặt bên hay trung đoạn của hình chóp đều:
\(d = SK = \sqrt {S{R^2} - K{R^2}} \)\(\, = \sqrt {{{20}^2} - {6^2}} = 2\sqrt {91} (cm)\)
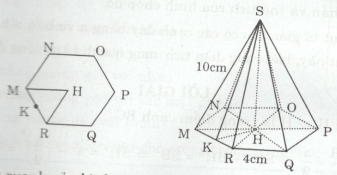
Diện tích xung quanh của hình chóp đều là:
\({S_{xq}} = p.d = {1 \over 2}.6MR.SK \)\(\,= 3.12.2\sqrt {91} = 72\sqrt {91} (c{m^2})\)
Diện tích toàn phần của hình chóp đều là:
\({S_{tp}} = {S_{xq}} + {S_d} = 72\sqrt {91} + 36\sqrt {108}\)\(\, \approx 1060,96(c{m^2})\)
