Bài tập - Chủ đề 3 : Hình lăng trụ đứng - Bài tập 7 trang 110 Tài liệu dạy – học Toán 8 tập 2. Giải bài tập Đường chéo của một hình hộp chữ nhật là đoạn nối hai đỉnh không thuộc bất cứ mặt bên hay mặt đáy nào. Chứng minh rằng độ dài đường chéo d được tính theo ba kích thước a, b, c bởi công thức:

Đường chéo của một hình hộp chữ nhật là đoạn nối hai đỉnh không thuộc bất cứ mặt bên hay mặt đáy nào. Chứng minh rằng độ dài đường chéo d được tính theo ba kích thước a, b, c bởi công thức:
\(d = \sqrt {{a^2} + {b^2} + {c^2}} \)

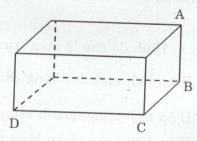
Xét ∆BCD vuông tại C ta có
\(B{D^2} = D{C^2} + B{C^2}\) (định lí Py-ta-go)
Advertisements (Quảng cáo)
Xét ∆DBA vuông tại B ta có:
\(D{A^2} = A{B^2} + B{D^2}\) (định lí Py-ta-go)
Do đó \(D{A^2} = A{B^2} + D{C^2} + B{C^2} \)\(\,= {c^2} + {a^2} + {b^2}\)
\( \Rightarrow {d^2} = {a^2} + {b^2} + {c^2} \)
\(\Rightarrow d = \sqrt {{a^2} + {b^2} + {c^2}} \)
