
Chứng minh trung điểm của các cạnh của một ngũ giác đều tạo thành một ngũ giác đều.

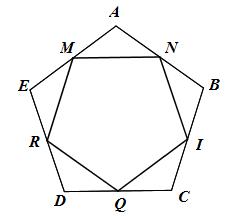
M, N, P, Q, R lần lượt là trung điểm của các cạnh EA, AB, BC, CD, DE của hình ngũ giác đều
\( \Rightarrow EM = MA = AN = NB = NP = PC = CQ = QD = DR = RE\)
Mặt khác \(\widehat A = \widehat B = \widehat C = \widehat D = \widehat E\) (ABCDE là ngũ giác đều)
Do đó \(\Delta AMN = \Delta BNP = \Delta CPQ = \Delta DQR = \Delta EMR\)
\( \Rightarrow MN = NP = PQ = QR = MR\,\,\left( 1 \right)\)
Advertisements (Quảng cáo)
Ta có \(\widehat {RMN} + \widehat {EMR} + \widehat {AMN} = {180^0}\) (E M, A thẳng hàng),
\(\widehat {MNP} + \widehat {ANM} + \widehat {BNP} = {180^0}\) (A, N, B thẳng hàng)
Và \(\widehat {EMR} = \widehat {AMN} = \widehat {ANM} = \widehat {BNP}\)
\(\left( {\Delta EMR = \Delta AMN = \Delta BNP} \right) \Rightarrow \widehat {RMN} = \widehat {MNP}\)
Lần lượt chứng minh tương tự ta có:
\(\widehat {RMN} = \widehat {MNP} = \widehat {NPQ} = \widehat {PQR} = \widehat {MRQ}\,\,\left( 2 \right)\)
Từ (1) và (2) suy ra đa giác MNPQR là ngũ giác đều.
