
Chứng minh rằng trong một ngũ giác, tổng các đường chéo lớn hơn chu vi.

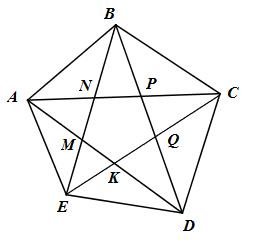
Xét ngũ giác ABCDE cần chứng minh rằng:
\(AC + A{\rm{D}} + BD + BE + CE > AB + BC + CD + DE + EA\)
Gọi M, N lần lượt là giao điểm của BE và AD, AC.
P, Q lần lượt là giao điểm của BD với AC, CE.
K là giao điểm của CE và AD.
Advertisements (Quảng cáo)
\(\Delta NAB\) có \(AN + BN > AB\) (BĐT tam giác)
Tương tự \(\Delta PBC\) có \(BP + CP > BC,\,\,\Delta QCD\) có \(CQ + DQ > CD\)
\(\Delta KDE\) có \(DK + EK > DE,\,\,\Delta MAE\) có \(AM + EM > EA\)
Do đó \(AN + BN + BP + CP + CQ + DQ + DK + EK + AM + EM > AB + BC + CD + DE + EA\)
Mà
\(\eqalign{ & AC + AD + BD + BE + CE \cr & > \left( {AN + CP} \right) + \left( {DK + AM} \right) + \left( {BP + DQ} \right) + \left( {EM + BN} \right) + \left( {CQ + EK} \right) \cr & = AN + CP + DK + AM + BP + DQ + EM + BN + CQ + EK \cr & = AN + BN + BP + CP + CQ + DQ + DK + EK + AM + EM \cr} \)
Vậy \(AC + A{\rm{D}} + BD + BE + CE > AB + BC + CD + DE + EA\)
