
Cho hình vuông ABCD có cạnh là a và O là giao điểm của hai đường chéo, vẽ điềm M trên cạnh AB và điểm N trên cạnh BC sao cho góc MON vuông. Tính theo a diện tích tứ giác MONB

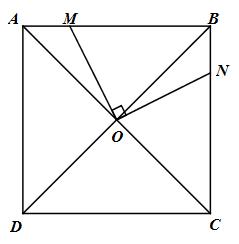
Tứ giác ABCD là hình vuông \( \Rightarrow OA = OB = {1 \over 2}AC = {1 \over 2}BD\)
\(\eqalign{ & \widehat {AOB} = {90^0},\,\,\widehat {OAB} = \widehat {OBA} = {45^0} \cr & {S_{OAB}} = {1 \over 2}.OA.OB = {1 \over 2}.{1 \over 2}AC.{1 \over 2}BD = {1 \over 4}{S_{ABCD}} = {1 \over 4}{a^2} \cr} \)
Xét \(\Delta OAM\) và \(\Delta OBN\) ta có: \(OA = OB,\)
Advertisements (Quảng cáo)
\(\widehat {OAM} = \widehat {OBN}\,\,\left( { = {{45}^0}} \right)\) và \(\widehat {AOM} = \widehat {BON}\) (hai góc cùng phụ với \(\widehat {MOB}\()
Do đó \(\Delta OAM = \Delta OBN\,\,\,\left( {g.c.g} \right)\)
\( \Rightarrow {S_{OAM}} = {S_{OBN}}\)
Do đó \({S_{OAM}} + {S_{OMB}} = {S_{OBN}} + {S_{OMB}} \Rightarrow {S_{AOB}} = {S_{MONB}}\)
Vậy \({S_{MONB}} = {1 \over 4}{a^2}\)
