
a) Hãy chứng minh AB // A’B’ và tính độ dài AB trong hình dưới.
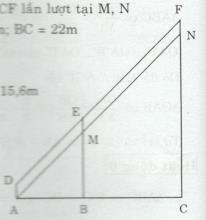
b) Hãy tính chiều cao của cây cao nhất trong hình vẽ dưới đây.
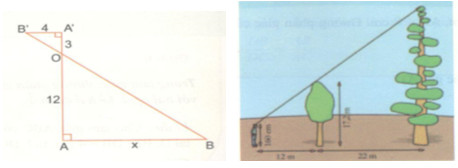

a)\(AB \bot AA'(gt),A’B’ \bot AA'(gt)\)
\(\Rightarrow AB//A’B’\)
∆OAB có AB // A’B’ \( \Rightarrow \dfrac{{A’B’}}{{AB}} = \dfrac{{OA’}}{{OA}}\) (Hệ quả của định lí Thales)
Nên \(\dfrac{4}{x} = \dfrac{3}{{12}} \)\(\;\Rightarrow x = \dfrac{{4.12}}{3} = 16\)
b) Đặt tên các vị trí như như hình bên
Qua A vẽ đường thẳng song song với DE, cắt BE, CF lần lượt tại M, N
Advertisements (Quảng cáo)
Ta có \(AD =160cm = 1,6m; BE = 17,2m; \)\(\,AB = 12m; BC = 22m\)
Do đó AC = AB + BC = 34m
Các tứ giác ADEM, MEFN là hình bình hành
Nên \(EM = FN = AD = 1,6m \)
\(\Rightarrow BM = BE – EM = 15,6m\)
∆CAN có BM//CN
\(\dfrac{{BM}}{{CN}} = \dfrac{{AB}}{{AC}}\) (Hệ quả của định lí Thales)
Nên \(\dfrac{{15,6}}{{CN}} = \dfrac{{12}}{{34}}\)
\(\Rightarrow CN = \dfrac{{15,6.12}}{{34}} = 44,2(m)\)
\( \Rightarrow CF = CN + FN = 44,2 + 1,6 \)\(\,= 45,8(m)\)
Vậy chiều cao của cây cao nhất trong hình vẽ là 45,8 m
