Bài 10 trang 63 - Sách giáo khoa môn Toán 8 tập 2, Bài 10 Tam giác ABC có đường cao AH. Đường thẳng d song song với BC, cắt các cạnh AB,AC và đường cao AH theo thứ tự tại các điểm...

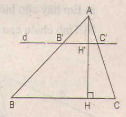
Bài 10 Tam giác ABC có đường cao AH. Đường thẳng d song song với BC, cắt các cạnh AB,AC và đường cao AH theo thứ tự tại các điểm B’, C’ và H'(h.16)

a) Chứng minh rằng:

\(\frac{AH'}{AH}\) = \(\frac{B'C'}{BC}\).

b) Áp dụng: Cho biết AH’ = \(\frac{1}{3}\) AH và diện tích tam giác ABC là 67.5 cm²

Tính diện tích tam giác AB’C’.

a) Chứng minh \(\frac{AH'}{AH}\) = \(\frac{B'C'}{BC}\) 

Vì B’C’ // với BC => \(\frac{B'C'}{BC}\) = \(\frac{AB'}{AB}\)            (1)

Trong ∆ABH có BH’ // BH => \(\frac{AH'}{AH}\) = \(\frac{AB'}{BC}\)  (2)

Từ 1 và 2 => \(\frac{B'C'}{BC}\) = \(\frac{AH'}{AH}\)

b) B’C’ // BC mà AH ⊥ BC nên AH’ ⊥ B’C’ hay AH’ là đường cao của tam giác AB’C’.

Áp dụng kết quả câu a) ta có: AH’ = \(\frac{1}{3}\) AH

\(\frac{B'C'}{BC}\) = \(\frac{AH'}{AH}\) = \(\frac{1}{3}\) => B’C’ = \(\frac{1}{3}\) BC

=> S_AB’C’= \(\frac{1}{2}\) AH’.B’C’ = \(\frac{1}{2}\).\(\frac{1}{3}\)AH.\(\frac{1}{3}\)BC

=>S_AB’C’= (\(\frac{1}{2}\)AH.BC)\(\frac{1}{9}\)

mà S_ABC= \(\frac{1}{2}\)AH.BC = 67,5 cm²

Vậy S_AB’C’= \(\frac{1}{9}\).67,5= 7,5 cm²