16. Cho tam giác ABC cân tại A, các đường phân giác BD, CE (D ∈ AC, E ∈ AB). Chứng minh rằng BEDC là hình thang cân có đáy nhỏ bằng cạnh bên.

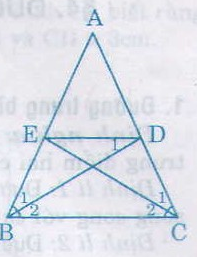
a) ∆ABD và ∆ACE có
AB = AC (gt)
\(\widehat{A}\) chung
\(\widehat{B_{1}}\) = \(\widehat{C_{1}}\) \(\left ( =\frac{1}{2}\widehat{B}=\frac{1}{2}\widehat{C} \right )\)
Nên ∆ABD = ∆ACE (g.c.g)
Advertisements (Quảng cáo)
Suy ra AD = AE
Chứng minh BEDC là hình thang cân như câu a của bài 15.
b) Vì BEDC là hình thang cân nên DE // BC.
Suy ra \(\widehat{_{D_{1}}}\) = \(\widehat{B_{2}}\) (so le trong)
Lại có \(\widehat{B_{2}}\) = \(\widehat{B_{1}}\) nên \(\widehat{B_{1}}\) = \(\widehat{_{D_{1}}}\)
Do đó tam giác EBD cân. Suy ra EB = ED.
Vậy BEDC là hình thang cân có đáy nhỏ bằng cạnh bên.
