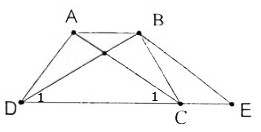
18. Chứng minh định lí "Hình thang có hai đường chéo bằng nhau là hình thang cân” qua bài toán sau: Cho hình thang ABCD (AB = CD) có AC = BD.
Qua B kẻ đường thẳng song song với AC, cắt đường thẳng DC tại E. Chứng mình rằng:
a) ∆BDE là tam giác cân.
b) ∆ACD = ∆BDC.
c) Hình thang ABCD là hình thang cân.

a) Hình thang ABEC (AB // CE) có hai cạnh bên AC, BE song song nên chúng bằng nhau:
AC = BE (1)
Theo giả thiết AC = BD (2)
Từ (1) và (2) suy ra BE = BD do đó tam giác BDE cân.
Advertisements (Quảng cáo)
b) Ta có AC // BE suy ra  =
= 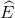 (3)
(3)
∆BDE cân tại B (câu a) nên 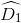 =
= 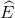 (4)
(4)
Từ (3) và (4) suy ra  =
= 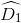
Xét ∆ACD và ∆BCD có AC = BD (gt)
 =
= 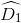 (cmt)
(cmt)
CD cạnh chung
Nên ∆ACD = ∆BDC (c.g.c)
c) ∆ACD = ∆BDC (câu b)
Suy ra 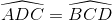
Hình thang ABCD có hai góc kề một đáy bằng nhau nên là hình thang cân.
