Cho hình thang cân ABCD (AB // CD), E là giao điểm của hai đường chéo. Chứng minh rằng EA = EB, EC = ED.. Bài 13 trang 74 sgk toán 8 tập 1 - Hình thang cân
13. Cho hình thang cân ABCD (AB // CD), E là giao điểm của hai đường chéo. Chứng minh rằng EA = EB, EC = ED.

Do ABCD là hình thang cân nên AD = BC, AC = BC, \(\widehat{D}=\widehat{C}\)
Xét hai tam giác ADC và BCD, ta có: 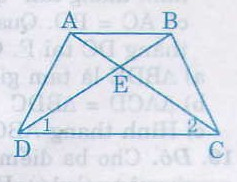
AD = BC (gt)
AC = BD (gt)
DC chung
Advertisements (Quảng cáo)
Nên ∆ADC = ∆BCD (c.c.c)
Suy ra \(\widehat{C_{1}}=\widehat{D_{1}}\)
Do đó tam giác ECD cân tại E, nên EC = ED
Ta lại có: AC = BD suy ra EA = EB
Chú ý: Ngoài cách chứng minh ∆ADC = ∆BCD (c.c.c) ta còn có thể chứng minh ∆ADC = ∆BCD (c.g.c) như sau:
AD = BC, \(\widehat{D}=\widehat{C}\) , DC là cạnh chung.
