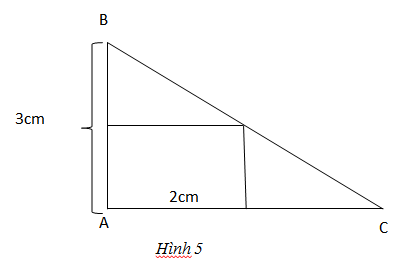
Đố: Lan có một miếng bìa hình tam giác ABC vuông tại A, cạnh AB = 3cm. Lan tính rằng nếu cắt từ miếng bìa đó ra một hình chữ nhật ấy có diện tích bằng một nửa diện tích của miếng bìa ban đầu. Tính độ dài cạnh AC của tam giác ABC.
Hướng dẫn làm bài:
Gọi x (cm) là cạnh AC (x > 0).
Gọi hình chữ nhật là MNPA thì MC = x – 2 (cm)
Vì MN // AB nên \({{MN} \over {AB}} = {{MC} \over {AC}}\)
=>\(MN = {{AB.MC} \over {AC}} = {{3\left( {x - 2} \right)} \over x}\)
Diện tích hình chữ nhật : \(2.{{3\left( {x - 2} \right)} \over x} = {{6\left( {x - 2} \right)} \over x}\)
Advertisements (Quảng cáo)
Diện tích hình tam giác :\({1 \over 2}AB.AC = {1 \over 2}.3x = {3 \over 2}x\)
Vì diện tích hình chữ nhật bằng một nửa diện tích hình tam giác
\({3 \over 2}x = 2{{6\left( {x - 2} \right)} \over x} \Leftrightarrow 3{x^2} = 24 - 48\)
⇔\(3{x^2} - 24x + 48 = 0\)
⇔\({x^2} - 8x + 16 = 0\)
⇔\({\left( {x - 4} \right)^2} = 0\)
⇔\(x = 4\) (thỏa điều kiện đặt ra)
Vậy AC = 4cm.
