Cho hình bình hành ABCD. Gọi E là điểm đối xứng với D qua điểm A, gọi F là điểm đối xứng với D qua điểm C. Chứng minh rằng điểm E đối xứng với điểm F qua điểm B.. Bài 52 trang 96 sgk toán 8 tập 1 - Đối xứng tâm
Bài 52. Cho hình bình hành \(ABCD\). Gọi \(E\) là điểm đối xứng với \(D\) qua điểm \(A\), gọi \(F\) là điểm đối xứng với \(D\) qua điểm \(C\). Chứng minh rằng điểm \(E\) đối xứng với điểm \(F\) qua điểm \(B\).
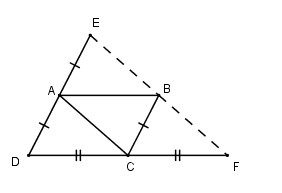
\(AE // BC\) (vì \(AD // BC\))
\(AE = BC\) (cùng bằng \(AD\))
nên \(ACBE\) là hình bình hành theo dấu hiệu nhận biết hình bình hành.
Advertisements (Quảng cáo)
Suy ra: \(BE // AC, BE = AC\) (1)
Tương tự \(BF // AC, BF = AC\) (2)
\(BE\) và \(BF\) cùng song song với \(AC\) và cùng đi qua điểm \(B\) nên theo tiên đề Ơ -clit \(BE\) trùng \(BF\), hay \(B,E,F\) thẳng hàng.
Từ (1) và (2) \( BE = BF\) do đó \(B\) là trung điểm của \(EF\).
Vậy \(E\) đối xứng với \(F\) qua \(B\).