Bài 54. Cho góc vuông \(xOy\), điểm \(A\) nằm trong góc đó. Gọi \(B\) là điểm đối xứng với \(A\) qua \(Ox\), gọi \(C\) là điểm đối xứng với \(A\) qua \(Oy\). Chứng mình rằng điểm \(B\) đối xứng với điểm \(C\) qua \(O\).

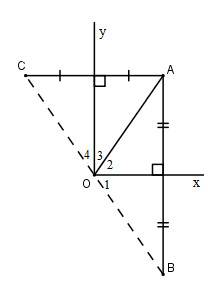
\(A\) đối xứng với \(B\) qua \(Ox\) và \(O\) nằm trên \(Ox\) nên \(OA\) đối xứng với \(OB\) qua \(Ox\) suy ra \(OA = OB\). (1)
Tam giác \(AOB\) cân tại \(O\) nên \(\widehat O_1=\widehat O_2\) (3)
\(A\) đối xứng với \(C\) qua \(Oy\) và \(O\) nằm trên \(Oy\) nên \(OA\) đối xứng với \(OC\) qua \(Oy\) suy ra \(OA = OC\) (2)
Advertisements (Quảng cáo)
Tam giác \(AOC\) cân tại \(O\) nên \(\widehat O_3=\widehat O_4\) (4)
Từ (1) và (2) suy ra \(OB = OC\) (*)
Từ (3) và (4) suy ra \(\widehat O_1+\widehat O_2+\widehat O_3+\widehat O_4=2(\widehat O_2+\widehat O_3)=2.90^0=180^0\)
Do đó \(B, O, C\) thẳng hàng (2*)
Từ (*) và (2*) suy ra \(B\) đối xứng với \(C\) qua \(O\).
