Trả lời câu hỏi 3 Bài 4 trang 16 Toán 8 Tập 2. Giải phương trình tích ta áp dụng công thức:. Bài 4. Phương trình tích

Giải phương trình:
\(\left( {x - 1} \right)\left( {{x^2} + 3x - 2} \right) - \left( {{x^3} - 1} \right) = 0\)
- Sử dụng hằng đẳng thức số 7:
\({A^3} - {B^3} = \left( {A - B} \right)\left( {{A^2} + AB + {B^2}} \right)\)
- Phân tích: \({x^3} - 1 = \left( {x - 1} \right)\left( {{x^2} + x + 1} \right)\)
Từ đó tìm được nhân tử chung là \((x-1)\), đưa phương trình về dạng phương trình tích.
Advertisements (Quảng cáo)
- Giải phương trình tích ta áp dụng công thức:
\(A(x).B(x) = 0\)
\(⇔ A(x) = 0\) hoặc \(B(x) = 0\)

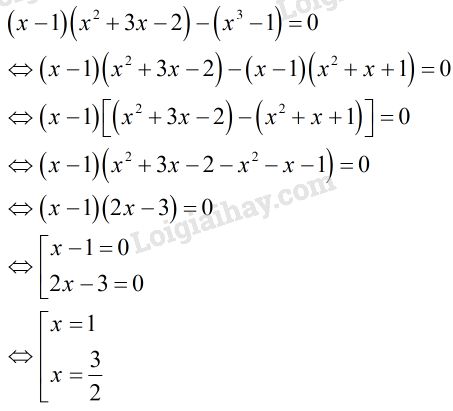
Vậy tập nghiệm của phương trình là \(S = \left\{ {1;\dfrac{3}{2}} \right\}\)
