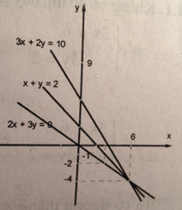
Vẽ hai đường thẳng \(\left( {{d_1}} \right):x + 2y = 2\) và \(\left( {{d_2}} \right):2x + 3y = 0\)
Hỏi đường thẳng \(\left( {{d_3}} \right):3x + 2y = 10\) có đi qua giao điểm của \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) hay không?

Vẽ đường thẳng \({d_1}\) là đồ thị của hàm số \(y = - x + 2\)
Cho \(x = 0 \Rightarrow y = 2\) (0; 2)
Cho \(y = 0 \Rightarrow x = 2\) (2; 0)
Vẽ đường thẳng \({d_2}\) là đồ thị của hàm số \(y = - {2 \over 3}x\)
Đồ thị đi qua O(0; 0)
Advertisements (Quảng cáo)
Cho \(x = 3 \Rightarrow y = - 2\) (3; -2)
Hai đường thẳng có hệ số góc khác nhau chúng cắt nhau tại B(6; -4)
Thay tọa độ của điểm B vào vế trái phương trình đường thẳng \({d_3}\) ta có:
\(3.6 + 2.\left( { - 4} \right) = 18 - 8 = 10\)
Tọa độ của điểm B nghiệm đúng phương trình đường thẳng \({d_3}\)
Vậy đường thẳng \({d_3}:3x + 2y = 10\) đi qua giao điểm của \({d_1}\) và \({d_2}\).