Cho tam giác ABC, các đường cao BH và CK. Chứng minh rằng:
a) Bốn điểm B, C, H, K cùng thuộc một đường tròn;
. Câu 15 trang 158 Sách bài tập (SBT) Toán 9 Tập 1 - Bài 2. Đường kính và dây của đường tròn
a) Bốn điểm B, C, H, K cùng thuộc một đường tròn;
. Câu 15 trang 158 Sách bài tập (SBT) Toán 9 Tập 1 - Bài 2. Đường kính và dây của đường tròn
Cho tam giác ABC, các đường cao BH và CK. Chứng minh rằng:
a) Bốn điểm B, C, H, K cùng thuộc một đường tròn;
b) HK < BC.
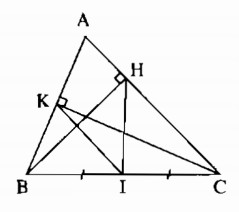
a) Gọi M là trung điểm của BC
Tam giác BCH vuông tại H có HM là đường
trung tuyến nên:
Advertisements (Quảng cáo)
\(HM = {1 \over 2}BC\) (tính chất tam giác vuông)
Tam giác BCK vuông tại K có KM là đường
trung tuyến nên:
\(KM = {1 \over 2}BC\) (tính chất tam giác vuông)
Suy ra: MB = MC = MH = MK.
Vậy bốn điểm B, C, H, K cùng nằm trên một đường tròn tâm M bán kính bằng \({1 \over 2}BC\).
b) Trong đường tròn tâm M ta có KH là dây cung không đi qua tâm, BC là đường kính nên: KH < BC.