Trong hình thang vuông ABCD với đáy là AD, BC có.... Câu 2.20. Trang 110 Sách Bài Tập (SBT) Toán 9 Tập 1 - Bài 2. Tỉ số lượng giác của góc nhọn
Trong hình thang vuông ABCD với đáy là AD, BC có \(\widehat A = \widehat B = 90^\circ \), \(\widehat {ACD} = 90^\circ ,BC = 4cm,AD = 16cm.\) Hãy tìm các góc C và D của hình thang.

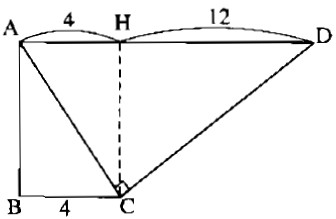
Kẻ đường cao CH của tam giác ACD vuông tại C. Khi đó:
Advertisements (Quảng cáo)
AH = BC = 4, HD = AD – AH = 12. Từ đó: HC2 = HA.HD = 48, vậy HC = \(4\sqrt 3 \).
Trong tam giác vuông HCD, ta có:
\(tgD = {{HC} \over {HD}} = {{4\sqrt 3 } \over {12}} = {{\sqrt 3 } \over 3} = tg30^\circ \) nên \(\widehat D = 30^\circ \). Suy ra: \(\widehat {BCD} = 180^\circ - 30^\circ = 150^\circ .\)
