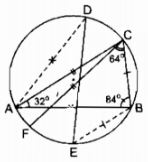
Cho tam giác ABC nội tiếp trong đường tròn tâm O, biết \(\widehat A = {32^0}\), \(\widehat B = {84^0}\). Lấy các điểm D, E, F thuộc đường tròn tâm O sao cho AD = AB, BE = BC, CF = CA. Hãy tính các góc của tam giác DEF.
Giải
\(\widehat A = {1 \over 2}\) sđ \(\overparen{BC}\) (tính chất góc nội tiếp)
\( \Rightarrow \) sđ \(\overparen{BC}\) \( = 2\widehat A = {2.32^0} = {64^0}\)
BC = BE (gt)
\( \Rightarrow \) sđ \(\overparen{BC}\) = sđ \(\overparen{BE}\) = 640
\(\widehat B = {1 \over 2}\) sđ \(\overparen{AC}\) (tính chất góc nội tiếp)
\( \Rightarrow \) sđ \(\overparen{AC}\) \( = 2\widehat B = {2.84^0} = {168^0}\)
AC = CF (gt)
\( \Rightarrow \) sđ \(\overparen{CF}\) = sđ \(\overparen{AC}\) = 1680
sđ \(\overparen{AC}\) + sđ \(\overparen{AF}\) + sđ \(\overparen{CF}\) = 3600
\( \Rightarrow \) sđ \(\overparen{AF}\) \( = {360^0} - \) sđ \(\overparen{AC}\) - sđ \(\overparen{CF}\) = 3600 – 1680. 2 = 240
Advertisements (Quảng cáo)
Trong ∆ABC ta có: \(\widehat A + \widehat B + \widehat C = {180^0}\)
\( \Rightarrow \widehat {ACB} = {180^0} - \left( {\widehat A + \widehat B} \right)\)
= \({180^0} - \left( {{{32}^0} + {{84}^0}} \right) = {64^0}\)
sđ \(\widehat {ACB} = {1 \over 2}\) sđ \(\overparen{AB}\)
\( \Rightarrow \) sđ \(\overparen{AB}\) \( = 2\widehat {ACB} = {2.64^0} = {128^0}\)
AD = AB (gt)
\( \Rightarrow \) sđ \(\overparen{AD}\) = sđ \(\overparen{AB}\) = 1280
\(\widehat {FED} = {1 \over 2}\) sđ \(\overparen{DF}\) \( = {1 \over 2}\) ( sđ \(\overparen{AD}\) + sđ \(\overparen{AF}\))
= \({1 \over 2}.\left( {{{128}^0} + {{24}^0}} \right) = {76^0}\)
\(\widehat {EDF} = {1 \over 2}\) sđ \(\overparen{EF}\) = \({1 \over 2}\) ( sđ \(\overparen{AB}\) - sđ \(\overparen{AF}\) - sđ \(\overparen{BE}\)
= \({1 \over 2}.\left( {{{128}^0} - {{24}^0} - {{64}^0}} \right) = {20^0}\)
\(\widehat {DFE} = {180^0} - \left( {\widehat {FED} + \widehat {EDF}} \right)\)
= \({180^0} - \left( {{{76}^0} + {{20}^0}} \right) = {84^0}\).
