Cho phương trình \({1 \over 2}{x^2} - 2x + 1 = 0\)
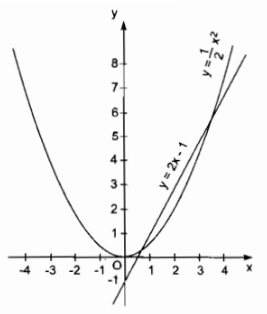
a) Vẽ đồ thị của hàm số \(y = {1 \over 2}{x^2}\) và \(y = 2x - 1\) trên cùng một mặt phẳng tọa độ. Dùng đồ thị tìm giá trị gần đúng nghiệm của phương trình (làm tròn đến chữ số thập phân thứ hai).
b) Giải phương trình đã cho bằng công thức nghiệm, so sánh với kết quả tìm được trong câu a.

a) Vẽ đồ thị \(y = {1 \over 2}{x^2}\)
|
x |
-2 |
-1 |
0 |
1 |
Advertisements (Quảng cáo) 2 |
| \(y = {1 \over 2}{x^2}\) |
2 |
0 |
2 |
Vẽ đồ thị y = 2x – 1
Cho x = 0 ⇒ y = -1(0; -1)
\({x_1} \approx 0,60;{x_2} \approx 3,40\)
b) \({1 \over 2}{x^2} - 2x + 1 = 0\)
\(\eqalign{
& \Leftrightarrow {x^2} - 4x + 2 = 0 \cr
& \Delta = {\left( { - 4} \right)^2} - 4.1.2 = 16 - 8 = 8 > 0 \cr
& \sqrt \Delta = \sqrt 8 = 2\sqrt 2 \cr
& {x_1} = {{4 + 2\sqrt 2 } \over {2.1}} = 2 + \sqrt 2 \approx 3,41 \cr
& {x_2} = {{4 - 2\sqrt 2 } \over {2.1}} = 2 - \sqrt 2 \approx 0,59 \cr} \)
