Cho tam giác ABC vuông tại A. Kẻ đường cao AH. Tính sinB, sinC trong mỗi trường hợp sau (làm tròn đến chữ số thập phân thứ tư), biết rằng:
a) AB = 13; BH = 5.
b) BH = 3; CH = 4.

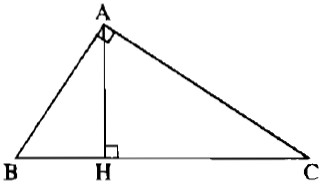
a) Xét tam giác vuông ABH, ta có: \(\cos \widehat B = {{BH} \over {AB}} = {5 \over {13}}\)
Tam giác ABC vuông tại A nên: \(\widehat B + \widehat C = 90^\circ \)
Suy ra: \(\sin \widehat C = c{\rm{os}}\widehat B = {5 \over {13}} = 0,3864.\)
Áp dụng định lí Pi-ta-go, ta có:
\(A{B^2} = A{H^2} + B{H^2} \Rightarrow A{H^2} = A{B^2} - B{H^2} = {13^2} - {5^2} = 144\)
Advertisements (Quảng cáo)
Suy ra: AH = 12
Ta có: \(\sin B = {{AH} \over {AB}} = {{12} \over {13}} \approx 0,9231\)
b) Ta có:
\(BC = BH + HC = 3 + 4 = 7\)
Theo hệ thức liên hệ giữa góc vuông và hình chiếu, ta có:
\(A{B^2} = BH.BC \Rightarrow AB = \sqrt {BH.BC} = \sqrt {3.7} = \sqrt {21} \)
\(\eqalign{
& A{C^2} = CH.BC \cr
& \Rightarrow AC = \sqrt {CH.BC} = \sqrt {4.7} = \sqrt {28} = 2\sqrt 7 \cr} \)
Suy ra: \(\sin \widehat B = {{AC} \over {BC}} = {{2\sqrt 7 } \over 7} \approx 0,7559\)
\(\sin \widehat C = {{AB} \over {BC}} = {{\sqrt {21} } \over 7} \approx 0,6547\)
