Câu 3.1 trang 103 Sách Bài Tập (SBT) Toán 9 Tập 2
Mỗi câu sau đây đúng hay sai
(A) Góc nội tiếp là góc tạo bởi hai dây của đường tròn đó.
(B) Trong một đường tròn, hai góc nội tiếp bằng nhau thì cùng chắn một cung.
(C) Trong một đường tròn, hai góc nội tiếp không cùng chắn một cung thì không bằng nhau.
(D) Trong một đường tròn, số đo của một góc nội tiếp bằng số đo cung bị chắn.
(E) Trong một đường tròn, góc nội tiếp có số đo bằng nửa số đo của góc ở tâm cùng chắn một cung.
Giải
Chọn câu đúng (E) Trong một đường tròn, góc nội tiếp có số đo bằng nửa số đo của góc ở tâm cùng chắn một cung.
Câu 3.2 trang 103 Sách Bài Tập (SBT) Toán 9 Tập 2
Cho nửa đường tròn đường kính AB, tâm O. Đường tròn tâm A bán kính AO cắt nửa đường tròn đã cho tại C. Đường tròn tâm B bán kính BO cắt nửa đường tròn đã cho tại D.
Đường thẳng qua O và song song với AD cắt nửa đường tròn đã cho tại E.
a) \(\widehat {ADC}\) và \(\widehat {ABC}\) có bằng nhau không? Vì sao?
b) Chứng minh CD song song với AB.
c) Chứng minh AD vuông góc với OC
d) Tính số đo của \(\widehat {DAO}\).
e) So sánh hai cung BE và CD.
Giải
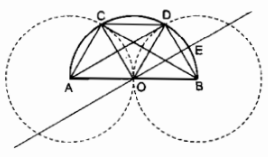
a) Trong đường tròn (O) ta có:
\(\widehat {ADC} = \widehat {ABC}\) (2 góc nội tiếp cùng chắn cung \(\overparen{AC}\))
b) ∆ACB nội tiếp trong đường tròn (O) có AB là đường kính nên ∆ABC vuông tại C
\( \Rightarrow CO = OA = {1 \over 2}AB\) (tính chất tam giác vuông)
AC = AO (bán kính đường tròn (A))
Suy ra: AC = AO = OC
\( \Rightarrow \) ∆ACO đều \( \Rightarrow \widehat {AOC} = {60^0}\)
∆ADB nội tiếp trong đường tròn đường kính AB nên ∆ADB vuông tại D
Advertisements (Quảng cáo)
\( \Rightarrow DO = OB = OA = {1 \over 2}AB\) (tính chất tam giác vuông)
BD = BO(bán kính đường tròn (B))
Suy ra: BO = OD = BD
\( \Rightarrow \) ∆BOD đều
\( \Rightarrow \widehat {ODB} = \widehat {BOD} = {60^0}\)
\(\widehat {AOC} + \widehat {COD} + \widehat {BOD} = {180^0}\)
Suy ra: \(\widehat {COD} = {60^0}\)
OC = OD (vì cùng bằng \({1 \over 2}AB\))
Suy ra: ∆COD đều
\( \Rightarrow \widehat {ODC} = {60^0} \Rightarrow \widehat {ODC} = \widehat {BOD}\)
\( \Rightarrow \) CD // AB (vì có cặp góc ở vị trí so le trong bằng nhau)
c) ∆AOC đều (chứng minh trên) \( \Rightarrow OA = AC = OC\)
∆OCD đều (chứng minh trên) \( \Rightarrow OC = OD = CD\)
Suy ra: AC = AO = OD = DC
Vậy: tứ giác AODC là hình thoi.
d) ∆BOD đều (chứng minh trên) \( \Rightarrow \widehat {OBD} = {60^0}\) hay \(\widehat {ABD} = {60^0}\)
∆ADBvuông tại D
\( \Rightarrow \widehat {DAB} + \widehat {ABD} = {90^0}\) \( \Rightarrow \widehat {DAB} = {90^0} - \widehat {ABD} = {90^0} - {60^0} = {30^0}\)
Vậy \(\widehat {DAO} = {30^0}\)
e) OE // AD (gt)
\( \Rightarrow \widehat {EOB} = \widehat {DAO} = {30^0}\) (hai góc đồng vị)
sđ \(\overparen{BE}\) \( = \widehat {EOB} = {30^0}\)
sđ \(\overparen{CD}\) \( = \widehat {COD}\)
mà \(\widehat {COD} = {60^0}\) (chứng minh trên)
sđ \(\overparen{CD}\) = 600
Suy ra: Số đo cung \(\overparen{CD}\) gấp đôi số đo cung \(\overparen{BE}\).
