Dựng tam giác ABC, biết BC = 3 cm, \(\widehat A = {45^0}\) và trung tuyến AM = 2,5 cm.
Giải
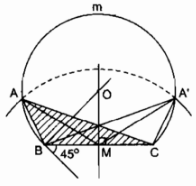
Cách dựng
− Dựng đoạn BC = 3cm
− Dựng \(\widehat {CBx} = 45^\circ \)
− Dựng trung điểm M của BC
− Dựng trung trực BC
Advertisements (Quảng cáo)
− Dựng tia vuông góc Bx tại B cắt đường trung trực BC tại O.
− Dựng cung tròn \(\overparen{BmC}\) bán kính OB là cung chứa góc 45º vẽ trên BC.
− Dựng cung tròn tâm M bán kính 2,5 cm cắt cung \(\overparen{BmC}\) tại A và A¢.
− Nối AB, AC (hoặc A’B, A’C) ta có ∆ABC (hoặc ∆A’BC) thỏa mãn điều kiện bài toán.
Vì BC = 3 cm, nên bán kính OB = \({{3\sqrt 2 } \over 2}\) (cm).
Khoảng cách 2 tâm MO = \({{3\sqrt 2 } \over 2}\) (cm)
\({{3\sqrt 2 } \over 2} - 2,5 < MO < {{3\sqrt 2 } \over 2} + 2,5\) nên (O) và (M) luôn cắt nhau. Bài toán luôn dựng được.
