Cho nửa đường tròn đường kính AB và C là một điểm trên nửa đường tròn. Trên bán kính OC lấy điểm D sao cho OD bằng khoảng cách CH từ C đến AB. Tìm quỹ tích các điểm D khi C chạy trên nửa đường tròn đã cho.
Giải
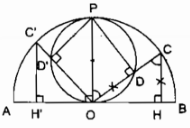
Chứng minh thuận:
Từ O kẻ đường thẳng vuông góc với AB cắt nửa đường tròn đường kính AB tại P. O cố định, đường tròn đường kính AB cố định suy ra P cố định.
Nối PD. Ta có: OP // CH (vì hai đường thẳng cùng vuông góc với AB)
Xét ∆OCH và ∆OPD:
OD = CH (gt)
OP = OC (bán kính)
\(\widehat {POD} = \widehat {OCH}\) (so le trong)
Suy ra: ∆DOP = ∆HCO (c.g.c)
Advertisements (Quảng cáo)
\( \Rightarrow \)\(\widehat {ODP} = \widehat {CHO}\) mà \(\widehat {CHO} = 90^\circ \) nên \(\widehat {ODP} = 90^\circ \)
Khi C chuyển động trên nửa đường tròn đường kính AB thì D thay đổi tạo với 2 đầu đoạn thẳng OP cố định một góc \(\widehat {OPD} = 90^\circ \). Vậy D chuyển động trên đường tròn đường kính OP.
Chứng minh đảo: Lấy điểm D¢ bất kỳ trên đường tròn đường kính OP. Kẻ OD’ cắt nửa đường tròn đường kính AB tại C’, kẻ C’H’⊥ AB ta phải chứng minh OD’ = C’H’.
Nối PD’. Xét ∆C’H’O và ∆PD’O
\(\widehat {C’H’O} = \widehat {PD’O} = 90^\circ \)
OC’ = OP (bán kính đường tròn tâm O)
\(\widehat {D’OP} = \widehat {OC’H’}\) (so le trong)
Suy ra: ∆C’H’O = ∆PD’O (cạnh huyền, góc nhọn)
\( \Rightarrow \) C’H’ = OD’
Vậy quỹ tích các điểm D khi C chuyển động trên nửa đường tròn đường kính AB là đường tròn đường kính OP.
