Trong mặt phẳng tọa độ, các đỉnh của tam giác ABC có tọa độ như sau: A(1 ; 1) ; B(5 ; 1) ; C(7 ; 9). Câu 36. Trang 108 Sách Bài Tập (SBT) Toán 9 Tập 1 - Bài 2. Tỉ số lượng giác của góc nhọn
Trong mặt phẳng tọa độ, các đỉnh của tam giác ABC có tọa độ như sau: A(1 ; 1) ; B(5 ; 1) ; C(7 ; 9)
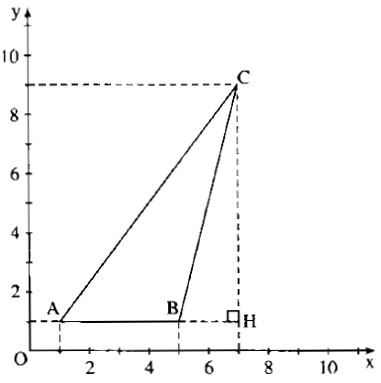
Hãy tính:
a) Giá trị của \(tg\widehat {BAC}\) (làm tròn đến chữ số thập phân thứ tư);
b) Độ dài của cạnh AC.
a) Vì tam giác ACH vuông tại H nên ta có:
Advertisements (Quảng cáo)
\(tg\widehat {HAC} = {{CH} \over {AH}} = {{9 - 1} \over {7 - 1}} = {8 \over 6} = 1,3333\)
Mà A, B, H thẳng hàng nên suy ra:
\(tg\widehat {BAC} = tg\widehat {HAC} = 1,3333\)
b) Áp dụng định lí Pi-ta-go vào tam giác vuông ACH, ta có:
\(A{C^2} = C{H^2} + A{H^2}\)
Suy ra: \(AC = \sqrt {C{H^2} + A{H^2}} = \sqrt {{8^2} + {6^2}} = \sqrt {100} = 10\)