Tam giác ABC vuông tại A, có \(AC = {1 \over 2}BC\). Tính :
\(\sin B,\cos B,tgB,\cot gB.\)

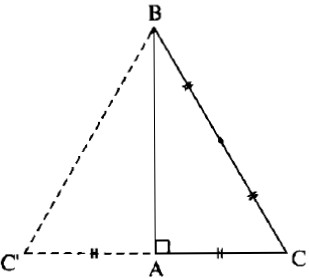
Áp dụng định lí Pi-ta-go vào tam giác vuông ABC, ta có:
\(B{C^2} = A{B^2} + A{C^2}\)
Advertisements (Quảng cáo)
\(\eqalign{
& \Rightarrow A{B^2} = B{C^2} - A{C^2} \cr
& = B{C^2} - {{B{C^2}} \over 4} = {{3B{C^2}} \over 4} \cr
& \Rightarrow AB = {{BC\sqrt 3 } \over 2} \cr} \)
Vậy: \(\sin \widehat B = {{AC} \over {BC}} = {{{1 \over 2}BC} \over {BC}} = {1 \over 2}\)
\({\rm{cos}}\widehat B = {{AB} \over {BC}} = {{{{\sqrt 3 } \over 2}BC} \over {BC}} = {{\sqrt 3 } \over 2}\)
\(tg\widehat B = {{AC} \over {AB}} = {{{1 \over 2}BC} \over {{{\sqrt 3 } \over 2}BC}} = {{\sqrt 3 } \over 3}\)
\(\cot g\widehat B = {1 \over {tgB}} = {1 \over {{{\sqrt 3 } \over 3}}} = \sqrt 3 \)
