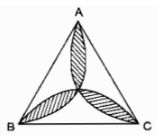
Trong một tam giác đều ABC (h.13), vẽ những cung tròn đi qua tâm của tam giác và từng cặp đỉnh của nó. Cho biết cạnh tam giác bằng a, tính diện tích hình hoa thị gạch sọc.
Giải
Diện tích hình hoa thị bằng tổng diện tích 3 hình viên phân trừ diện tích tam giác đều ABC.
Gọi O là tâm của tam giác đều ABC
\( \Rightarrow OA = OB = OC\)
Vì ∆ABC đều nên AO, BO, CO là phân giác của các góc \(\widehat A,\widehat B,\widehat C\)
\(\widehat {OAC} = \widehat {OCA} = {{{{60}^0}} \over 2} = {30^0}\)
\(\widehat {AOC} = {180^0} - \left( {{{30}^0} + {{30}^0}} \right) = {120^0}\)
\( \Rightarrow \) sđ \(\overparen{AOC}\) là tam giác đều nội tiếp trong đường tròn (O’; R)
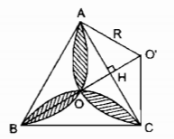
Trong tam giác O’HA có \(\widehat {O’HA} = {90^0}\), \(\widehat {HO’A} = {60^0}\)
AH = R.sin \(\widehat {HO’A} = R\). sin 600 = \({{R\sqrt 3 } \over 2}\)
Advertisements (Quảng cáo)
AC = 2AH = \(R\sqrt 3 \)
\( \Rightarrow R = {{AC} \over {\sqrt 3 }} = {a \over {\sqrt 3 }} = {{a\sqrt 3 } \over 3}\)
Squạt = \({{\pi {{\left( {{{a\sqrt 3 } \over 3}} \right)}^2}.120} \over {360}}\)
= \({{\pi {{{a^2}} \over 3}} \over 3} = {{\pi {a^2}} \over 9}\) (đơn vị diện tích)
∆O’HA có \(\widehat {O’HA} = {90^0}\); \(\widehat {HO’A} = {60^0}\)
O’A = \(R.\cos {60^0} = {{a\sqrt 3 } \over 3}.{1 \over 2} = {{a\sqrt 3 } \over 6}\)
S∆O’CA = \({1 \over 2}O’H.AC = {1 \over 2}.{{a\sqrt 3 } \over 6}.a = {{{a^2}\sqrt 3 } \over {12}}\) (đơn vị diện tích)
Sviên phân = Squạt – S∆O’CA = \({{\pi {a^2}} \over 9} - {{{a^2}\sqrt 3 } \over {12}} = {{4\pi {a^2} - 3{a^2}\sqrt 3 } \over {36}}\)
Diện tích tam giác đều ABC cạnh a: SABC = \({{{a^2}\sqrt 3 } \over 4}\) (đơn vị diện tích)
Diện tích hình hoa thị là:
S = 3Sviên phân - SABC = \(3.{{4\pi {R^2} - 3{a^2}\sqrt 3 } \over {36}} - {{{a^2}\sqrt 3 } \over 4}\)
= \({{4\pi {a^2} - 3{a^2}\sqrt 3 } \over {12}} - {{3{a^2}\sqrt 3 } \over {12}}\)
= \({{4\pi {a^2} - 6{a^2}\sqrt 3 } \over {12}} = {{{a^2}} \over 6}\left( {2\pi - 3\sqrt 3 } \right)\)
